Weiss By the Numbers: Going First in Weiss Schwarz

Author note: This is the culmination of a six month long research project detailed here and here. This post is somewhat math heavy, but you can safely skip the analysis sections if you’re not interested in how I came to my result

Introduction

Weiss Schwarz is a turn-based game, which naturally means someone gets to go first. The player who gets to go first gets the advantage of attacking once before the opponent can do anything and working with a deck before the opponent puts cards into inaccessible zones such as the clock. Logically, a first mover advantage could exist in Weiss Schwarz. If it exists, how good is this first mover advantage? Ideally, from a game balance standpoint, the effect should be slight. In a game where players compete on skill, imbalances in initial conditions should be mitigated to maximize ho much player skill impacts the outcome of the game[1]. For players, an absence of a detectable first mover advantage is a good thing.

This question is both simple and difficult to adjudicate. Weiss Schwarz’s method to determine who goes first removes major difficulties for statistical analysis. Unlike Pokémon or Magic: The Gathering where the player who wins the randomization gains the option of going first or second, Weiss players that win the randomization must go first. Thus, by removing the strategic element, Bushiroad gave me the ability to measure the pure effect of going first. Since you must go first, there exists no selection bias of good players making the correct choice and bad players making the incorrect choice to bias any estimation of the true effect.

All is not sunshine and rainbows. The context for which Weiss Schwarz is typically played, tournaments based on the Swiss pairing algorithm, adds additional difficulties. The Swiss algorithm matches players based on their performance, unlike the round robin which ensures everyone plays everyone within a group. Thus, games that are later in the tournament rely on the games prior to them. Observations are not independent and rely on the skill of players. These difficulties can be managed but will require a large data set to support. Luckily, I collected detailed information on 1,000 games played at Calgary locals to do just that. I evaluate the increased win rate using both simple methods and more advanced methods.

tl;dr

I find that going first increases the chance of victory by around twelve percentage points, i.e., an otherwise 50-50 match-up becomes a 56-44 match-up in favour of the player going first. This result is robust to player skill and set matchups.

I’ll start by describing the data. Then, I’ll walk through the simple method and discuss its deficiencies. Then I move to the core analytical tool, logistic regression, that controls for the round of Swiss and other consequential covariates, that allows us to evaluate whether going first truly causes the increased win rate. Finally, I discuss how this newfound knowledge can improve you as a Weiss Meister.

Data Set

I observed the weekly Friday Night Calgary Weiss Schwarz tournament at Sentry Box Cards for twenty-nine weeks starting on the 18^th of March 2022. The tournament consists of four rounds of games with match-ups determined by the Swiss tournament algorithm. The Calgary community plays mixed-language neo-standard Weiss, where English and Japanese sets adhere to their respective ban list. After each game I recorded the players, the set they played, who went first, and who won. I also included a match, week, and round identifier in the data set. Each tournament had on average nine games per round, resulting in 36 games per week and 1014 games in total. Thus, each match contains two players, two decks, a date, a round, a treatment (going first), and an outcome (win/loss). Due to the insistence of several players (myself included) to only throw Rock, Calgary players use other methods than Rock-Paper-Scissors to determine who goes first. Treatment is truly randomized.

Table 1: Summary Statistics and Weekly Conditional Probabilities

Players were randomly assigned to group A or group B based on the order their name appeared in the tournament software. Most players appeared in both groups about half the time, suggesting that the groups are balanced. Although this composition may matter for the simple method of estimating first mover advantage, it does not matter for the approach based on logistic regression assuming all relevant effects are controlled for. Further, A and B went first roughly half the time suggested balanced treatment between group A and group B. The roughly even win rates suggest that the groups are roughly balanced in terms of skill.

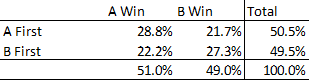
We can also present the combined data in a cross tab. The cross tab is presented from the perspective of players in group A, but if you read wins as losses, it becomes the crosstab from the perspective of player B. Of the 512 games where player A went first, they won 292 and lost 220. Group B tended to both lose more games and go second more often. Overall, the player that went first won notably more games than they lost. Interesting to know but that doesn’t tell us the effect of going first. We must devise an estimation strategy.

Estimating First Mover Advantage

Simple Method: Bayes Rule

The simplest method of estimating the first mover advantage is using basic definitions of probability. What we care about is the conditional probability of winning given a player went first. What is the chance that we win a game once we know that we went first? To find that, we simply apply Bayes Theorem:

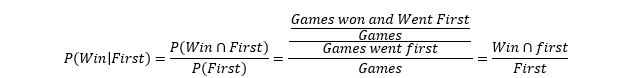
Formally, the conditional probability is the ratio of the joint probability of winning and going first divided by the probability of going first. Basically, we just take the ratio of the number of games we started and won over the number we went first. Thus, the conditional probability is a quick and dirty measure of the first mover advantage. If the conditional probability of winning given you went first is higher than your unconditional win rate, you have a first mover advantage.

We can carve up the sample a ton of ways and compute several estimates of the first mover advantage. This is one of the pros of using the simple method, I can easily look at subsamples due to how easy it is to compute. The easy computation also provides a simple interpretation. Further, it is agnostic about how the advantage comes about so it doesn’t need a ton of theory, a model, and doesn’t get tripped up when events are not independent[2]. The big con here is that this method does not control for anything. We likely suffer an omitted variable bias with this approach. Player skill, among other things, could drag up the observed effect of going first if more skilled players happen to go first more often or vice-versa even by random chance. However, the balanced groupings give me confidence that a simple estimator should be asymptotically unbiased.

Figure 1: Conditional Probability Distribution

I’ll present week-wise, group wise and an estimate the merges all the splits together. What you will notice is that the estimated conditional probabilities are all over the place based on the week, but the aggregated measures cluster closely and that the distribution of the conditional probabilities has a shape close to what you would expect. The weekly conditional probabilities range from a minimum of 40% in week 15 (several players who went first and lost apologized that week for “ruining my stats”) to 72% in week 12 (no players who went first and won apologized that week for “ruining my stats”). Most weeks, however, seemed to cluster between 50% and 60%, suggesting that the overall probability of winning given you went first is better than 50%. This is higher than the win rate for players in seat A or seat B in most given weeks, suggesting a counterfactual world where going first has no impact on winning is somewhat unlikely.

When we look at it simply from the perspective of players assigned to group A and players assigned group B for a particular match, the conditional probability is 57% for group A and 55% for group B. Again, higher than group A or group B’s overall win rate of around 50%. The overall probability of winning given you went first for both player A and player B is 56%, a full six percentage points higher than the overall win rate of both players of 50% (by construction). This looks indicative of a first mover advantage, but we should confirm using a formal test.

Formal Test of the simple method

I’ll introduce one more formal definition, statistical independence. Two events are statistically independent if the outcome of one event does not alter the outcome of another. Thus, if there is no going first advantage, the probability of winning given that you go first should be equal to the probability that you win. Thus, a test framework emerges:

We can take the sample stats and probabilities provided above and run a goodness-of-fit test to see if the H0 definition holds. If it does, we cannot say that a first mover advantage exists. Recall from the Idol Schwarz article, a goodness of fit test is a Chi-Squared test that compares observed outcomes versus what you would expect under the null. So, we compare the number of wins players going first and players going second got. If the result is like the pure win rate (50%), then we can’t reject the null of no first mover advantage. The observed data here is the cross tab in the data section. Our counterfactual is a crosstab like the one presented in the data section, but the cells are just the product of the columns and rows divided by the total number of games, which would be the result of a process where going first is completely independent from winning.

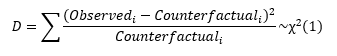
We’ll use a 5% significance value this time since we know the shape of the distribution of the counterfactual due to the nature of the test. We don’t have to worry about issues with the shape of the counterfactual distribution like last time.

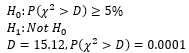
At this stage, we reject the null hypothesis that there is no first mover advantage is Weiss Schwarz. Players going first win more often in Weiss Schwarz.

Advanced Method: Logistic Regression

The simple method has two failure modes: it cannot parsimoniously control for other variables, and it cannot tell us how much of an advantage going first confers. Enter logistic regression. Logistic regression estimates the expected changes in odds of an event occurring given multiple independent variables. This allows us to estimate the effect of going first on the chance in winning parsimoniously. We use the following linear model:

Where y is the game outcome from the perspective of player A[3], beta is pre-transformed effect going first has on winning, and X is a set of controls. The model is estimated using a logistic function. Once converted out of logistic function space through the link function (which in our case is an exponential function so it’s easy) we can estimate the marginal effect of going first: i.e. how much does going first improve our win rate?

I estimate three models, each with more controls than the previous one. The first is the simplest, I regress the match result from the perspective of player A on whether they went first along with a set of fixed effects for which week it was to control for unobserved metagame differences and a set of fixed effects for the round of the tournament to control for any dependence introduced by the Swiss algorithm. Model 2 introduces a set of fixed effects for each player involved to pick up on skill differences and model three introduces set fixed effects to account for set quality independent of the pilot. Thus, we control for the unobserved effect of the Swiss tournament, matchups, and skill.

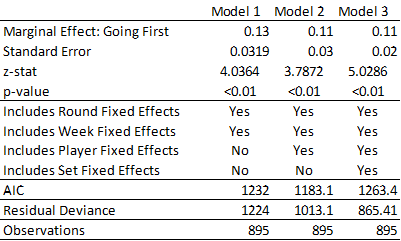
Before we discuss the results, let’s highlight the obvious: the regressions are calculated with less than the full 1000 game sample. Logistic regressions cannot be calculated in the presence of perfect prediction and perfect multicollinearity[4]. These phenomena occur when one of the controls is always associated with one realization of the outcome (perfect prediction) or one realization of the controls (perfect multicollinearity). Thus, I filtered the data to remove players who either never won or never lost, as well as removing players who only played one set and were the only players to play that set. I lost 105 observations in this manner[5].

All the models detect a going first advantage. They all find a statistically significant effect of going first on victory. The effect varies by model, but all the effects are close in size. The smallest point estimate suggests going first increases your chance to win by .11 percentage points (s.e. .02 points) while the largest suggests an increase of .13 percentage points (s.e. 0.03 points). Going first in Weiss Schwarz directly increases your chance of winning by about 12 percentage points, even when controlling for player quality and match-up. In other words, in a 50-50 match-up, the player going first has an expected win chance of 55-57% while the player going second has an expect win chance of 43-45%. It’s worth noting that controlling for the effect of set and player skill do slightly mitigate the going first advantage. This makes sense, good players and good sets can likely make more out of going first than bad players and bad sets, likely inflating the estimate of how good going first is.

How do I use this information?

Now that we know that going first in Weiss confers a notable advantage, how can you use that knowledge to your advantage? If going first gives you a bump in win rate, you might as well take advantage of it. In Calgary, we use methods of selecting who goes first that don’t involve rock-paper-scissors (RPS) because some of us REALLY like rock and we want to leave before the store closes. If you think you are better at RPS than most Weiss players, you should ask to play RPS. If you think you are poor at RPS, pull out the going first/going second cards. Most players do not seem to have a strong preference between the two so you will probably get your way if you take initiative.

Second, it broadens the way you think about the game. Hopefully it leads you to consider how your deck responds to going first and second in particular. Finally, I hope it spurs you to think of more things you want to know about Weiss, but can’t find an answer for. Some questions that immediately spring to mind:

I intentionally avoided trying to evaluate if certain decks do better going first and second. Every list someone floated to me included wildly different sets and builds. I was skeptical that any set preferred going second, appealed to ignorance and exchangibility and didn’t model it. I could be wrong!
I mentioned rigging up a multi level Baysean process to truly model a Swiss tournament in the proposal, but based on my appeal to asymptotics I decided it probably wouldn’t make a difference compared to a logistic regression that accounts for it.
I only show that going first matters. I don’t sketch out how the mechanism works! How does it cause a domino effect altering the whole game? Is it through concious pilot decisions or just altered luck?

This search process will deepen your appreciation for the game and teach you a few new tricks along the way.

Acknowledgements

I’d like to take this moment to thank the Calgary Weiss Community for putting up with me bothering them after every weird win and painful loss over the last year. Without them, this project would not have gotten off the ground. Specifically, I’d like to thank our tournament organizer, AnzuP. His patience and willingness to let me compare notes with reported wins minimized data errors on my part. Any errors in this analysis are my own

I’d like to thank Tyler from Weeb Shortz. First for inspiring me to conduct this study, and second for providing additional data to work with. The data provided was used to validate my estimates.

Bonus: What we played

Figure A: Breakdown of sets played during the study

As you can see, we played a lot of jank, with Other being the largest category at over 800 of the 2000 odd decks observed, followed by Hololive making up 325.

[1] Pokémon has changed its going first procedure multiple times when they found going first was too beneficial.

[2] This method only requires the event space (games observed here) to be exhaustive and outcomes within the space are mutually exclusive. Games are mutually exclusive events since you cannot win and lose the same game. The event space is definitionally exhaustive.

[3] Since outcomes are symmetric, running the regression from the perspective of player B renders the same result.

[4] Perfect separation leads to massively inflated estimates due to the introduction of flat spots in the likelihood function, while perfect multicollinearity prevents the inversion of the independent variable matrix due to violation of the rank condition. Both also wreck our identification strategy. Boo.

[5] I also removed players and sets that showed up in less than 8 matches, two full tournaments, to remove issues with quasi-perfect separation.